Steady progress has been made in understanding how cells communicate in populations. Communication and quorum sensing are a dominant topic in biology. Surprisingly little work has been done to understand how communication and feedback influence the cell cycle coordination of growth and division. Working in yeast we have shown that population density and cell cycle dependent feedback of simple form appears to produce periodic population structure generically. The mathematical results, observed across a wide range of models, with and without randomness, suggest the phenomena is robust. Experimental evidence supports the mathematical modeling and the existence of pseudo-synchronized clusters of cells.
The main observation is that feedback that results in cell cycle advances and or delays of a subpopulation of cells causes the population density to become multimodal and clustered. The particular form of the feedbacks are patterned on biological knowledge of the mechanisms of intercellular communication via metabolites and pheromones. Despite this natural underpinning and the prevalence of these mechanisms in biology, very little mathematical attention has been devoted to feedback dynamics of this form. Our recent work shows that the size and location of signaling and responsive regions within the cell cycle influences the number of emergent clusters. This suggests a bifurcation picture in which the geometry of the cell cycle is more influential than the explicit form and strength of the feedback. By focusing narrowly on phenomenological models of feedback that involve density dependence and the geometry of the cell cycle we will make progress toward understanding the phenomenon of clustered solutions and lay the foundations of a bifurcation theory in this setting.
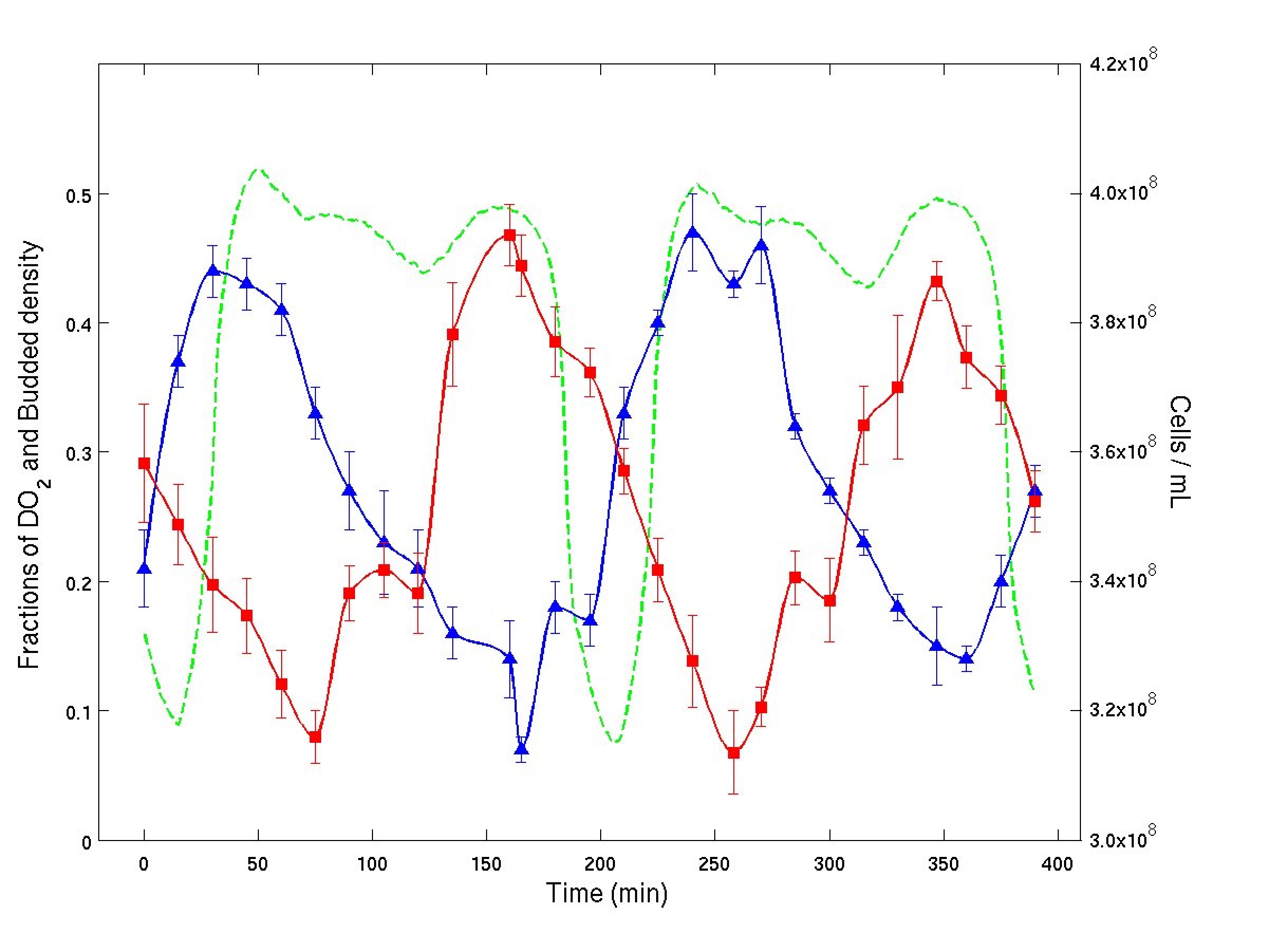
| In the plot to the right we show experimental time series from a continuous culture of budding yeast. Dissolved $O_2$ percentage (green), bud index percentage (blue) and cell density (red) are plotted versus elapsed time. The average cell cycle period as calculated from dilution rate was about 400 minutes. First we note that the cell cycle period, as calculated by the dilution rate, is approximately 400 minutes, and two $O_2$ oscillations occur during this period, suggesting that there may be two clusters. Next, analyzing the figure, we see that approximately half of the cells are budding at times (t = 50) and (t = 250), while at (t=170) less than 10% of the cells are budded. Each budding event is accompanied by a decrease in density (no cells are dividing) and followed by a sharp increase in cell density as these budded cells proceed through division. Note that at \(t=170\) since less than 10% of the cells are budded, most of the cells must be in the G1 phase of the cycle. When the bud index hits its next maximum at (t=250), approximately half of the cells must have budded. The other half of the cells must at that time still be in the G1 phase. As the cells that are budded then divide and the cell density increases, the cells that remained in G1 must still be in G1 since the bud index is again low. When the first group of cells has divided, the second group has been in G1 for at least 200 minutes. The next rise in bud index then must be due to these cells, since they have had time to mature, while the first group of recently divided cells clearly has not had time to reach budding again. Thus, these experiments show conclusively the existence of two clusters and that CDC clustering coexists with YAO. | 
|
We have shown several ways in which periodic population structures can be exploited in biology and bioprocess. The goals of this project are to develop and analyze a wide range of mathematical models that robustly develop clustered population structures to understand the essential features of this phenomenon.
The principal investigator for the project is Erik Bozcko of Vanderbilt University School of Medicine. The mathematical part of this research is coordinated by Todd Young and much of it occurs in the Department of Mathematics at Ohio University. The research group includes both undergraduate and graduate students, who are contributing to this project and developing valuable skills in applied mathematics. The students are also learning about the research process and developing their communication skills.
This work was supported by the National Science Foundation, National Institutes of Health, Joint DMS/NIGMS Initiative to Support Research in the Area of Mathematical Biology grant NIH-NIGMS 1R01GM090207-0109 during the years 2009-2013. Although this grant has expired, we still are actively pursuing this project.
The primary scientific goal is to deepen our understanding of the cell cycle in biological systems and how the cell cycle influences other biological process of cells and organisms. The role of the group at Ohio University is to develop mathematical tools for understanding the models that arise in the study of the cell cycle and other biological process that react with it. These mathematical goals are being pursued symbiotically with the biological goals. Biology has driven models and analysis of models has informed experiments.
By participating in this research project, students will learn specific mathematical and computational skills, learn about specific biological systems and how they can be modeled and also develop an understanding of how science and mathematics research works. Students range from advanced doctoral students to undergraduates and the experience of mentoring is a key goal. Students at all levels will develop the ability to express mathematical ideas, both in writing and oral presentations.
This project has many facets, from purely theoretical mathematical considerations, to very concrete programming tasks. The interests of individual students will be accommodated whenever possible. There are several levels at which you can participate, from exploratory to full-time research.
Anyone who wishes to can join the project for one quarter. You will learn more about the project, as well as develop valuable skills in mathematical writing, searching the literature, reading a research paper, presenting a seminar talk, and programming. I will learn about your strengths and weaknesses, and we both will learn how well you would fit into the research effort.
Each week we will have a group meeting where we will discuss what was accomplished on the project so far and what the next steps should be. As exploratory participants you will have a small task to complete each week. A sample weekly plan of other tasks for the quarter is as follows:
For graduate students in the Mathematics department, a limited number of paid research assistantships are available. In general, a student must participate at the exploratory level for one semester before being considered for a paid assistantship. For Ph.D. students, assistantships will generally support summer work on thesis research.
For undergraduate students, paid research assistantships are available for 5-10 hours per week, at an hourly rate of $10/hr. Credit for MATH 492 Undergraduate Research (Teir III equivalent) is available instead.
Each participant's research project will be determined to meet their interests and level. To help keep them on track and progressing toward the overall project's goals, there are the following specific expectations: