2 to the 9th Tensors¶
We now study the case of tensors with 
and 
.
At worst, the maximum rank is 
. By unfolding such a
tensor to a 
matrix, one can see that rank
is definitely achievable.
Visualizations over the Real numbers¶
A Specific Example¶
We are interested in analyzing the tensor
![L_9= \sum_{j=1}^d
\left(\bigotimes_{k=1}^{j-1}[1,0]\right)
\otimes [0,1] \otimes
\left(\bigotimes_{k=j+1}^{d}[1,0]\right)\,,](_images/math/5f042669ee4861c1edc17b54d25ffafc3bd4f4f7.png)
which has nominal rank 9. Consider the tensor-valued function
![G(t) =\bigotimes_{k=1}^{d}[1,t]](_images/math/de82c475620dc27f537d8491156cd91eaac80cc8.png)
and notice that the derivative of 
at 0 is 
, i.e.
.
Since
![G'(0) &=\lim_{h\rightarrow \infty} \frac{G(h)-G(0)}{h}\\
&=\frac{1}{h}\bigotimes_{k=1}^{d}[1,h]
-\frac{1}{h}\bigotimes_{k=1}^{d}[1,0]\,,](_images/math/7d1376de71d47d4233a44913ed9e3f5be7009a02.png)
we see that is a limit of rank 2 tensors.
(To avoid loss-of-precision errors due to cancellation, larger rank is
needed; see [BEY-MOH2005].)
To visualize , we choose
![T_1&=\sum_{j=1}^3
\left(\bigotimes_{k=1}^{j-1}[1,0]\right)
\otimes [0,1] \otimes
\left(\bigotimes_{k=j+1}^{d}[1,0]\right),\\
T_2&=\sum_{j=4}^6
\left(\bigotimes_{k=1}^{j-1}[1,0]\right)
\otimes [0,1] \otimes
\left(\bigotimes_{k=j+1}^{d}[1,0]\right),\quad\text{and}\\
T_3&=\sum_{j=7}^9
\left(\bigotimes_{k=1}^{j-1}[1,0]\right)
\otimes [0,1] \otimes
\left(\bigotimes_{k=j+1}^{d}[1,0]\right)\,,](_images/math/f2bcb7abab86252df3b84ca3daedb13c8678c0c4.png)
so that will be in the center of these three tensors.
Since these three tensors are in 
, any tensor
on the line connecting any two of them is in 
, and a tensor
in the plane is generically in 
.
We first produce a visualization of 
on
![[-1,2]\times[-1,2]](_images/math/ea61045a4371f2a1c81de0708a04d9b9278331ec.png)
, and obtain
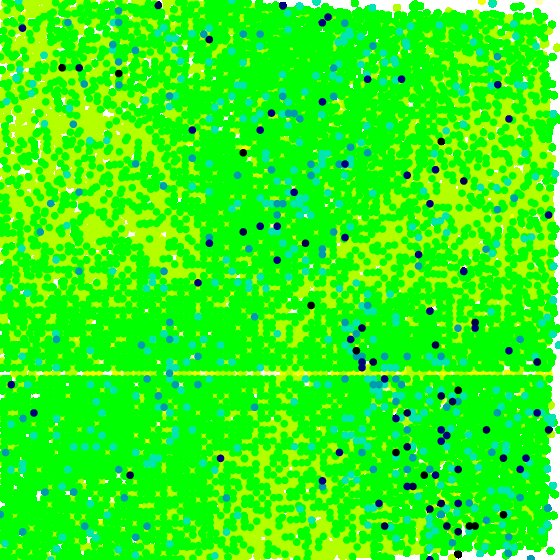
[data file 2to9pr2L9.dat]
Black points are scattered sparsely on
the visualization, but without apparent voids. It appears that the ALS
routine had some difficulty (with its fixed number of
iterations). There is a light horizontal streak along the line
connecting 
to 
of unknown cause, probably a
numerical artifact.
Next, we produce a visualization of , and obtain
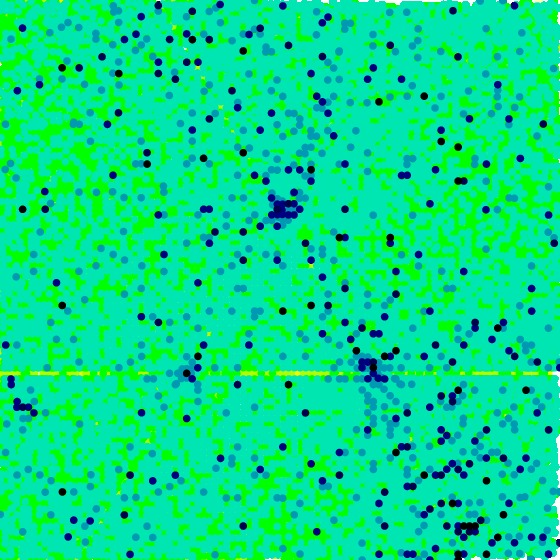
[data file 2to9pr3L9.dat]
Next, we produce a visualization of , which includes the
lines connecting any two of our base tensors, and obtain
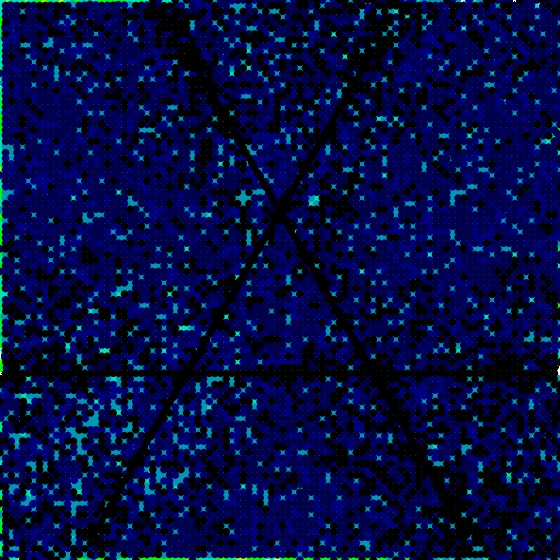
[data file 2to9pr6L9.dat]
A Random Example¶
To complement the specific example above,
we choose , 
, and randomly in
. Since these three tensors are in , any tensor
on the line connecting any two of them is in , and a tensor
in the plane is generically in .
We first produce a visualization of on
, and obtain
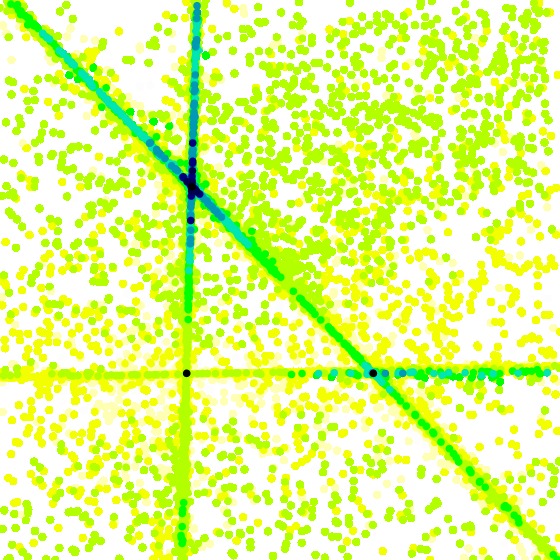
[data file 2to9pr3random.dat]
Next, using the same set of random , , and
, we produce a visualization of , and obtain
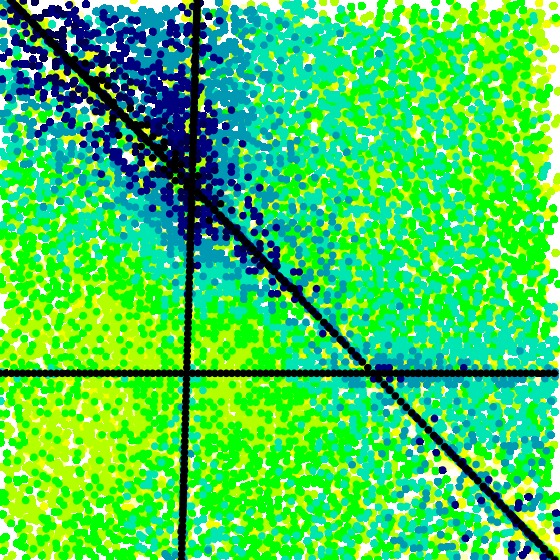
[data file 2to9pr6random.dat] Since in neither case do we find any unexpected black points, we conclude that the specific example above is not typical.
A Second Random Example¶
To complement the specific example above,
we choose , , and randomly in
. Since these three tensors are in , any tensor
on the line connecting any two of them is in 
, and a tensor
in the plane is generically in 
.
We first produce a visualization of on
, and obtain
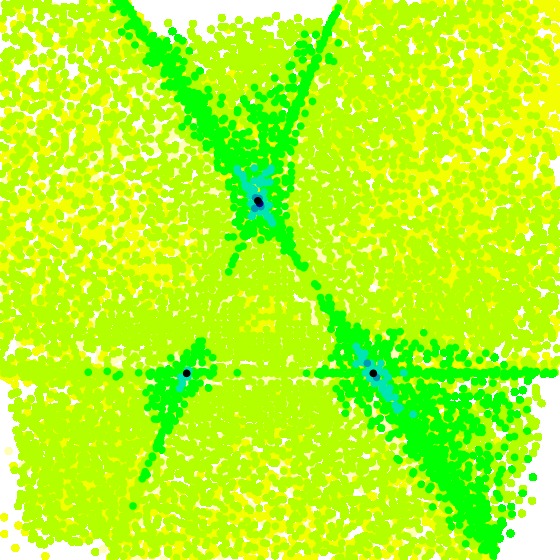
[data file 2to9pr16random2.dat]
Next, using the same set of random , , and
, we produce a visualization of , and obtain
[data file 2to9pr32random2.dat]
Next, using the same set of random , , and
, we produce a visualization of 
, and obtain
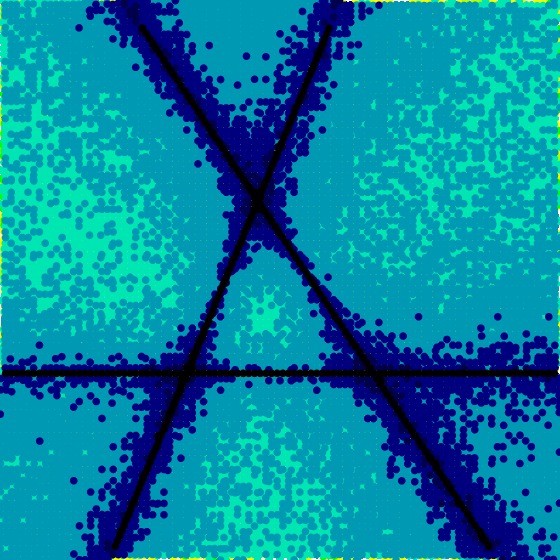
[data file 2to9pr40random2.dat]
Finally, we produce a visualization of , which should be
black, and obtain
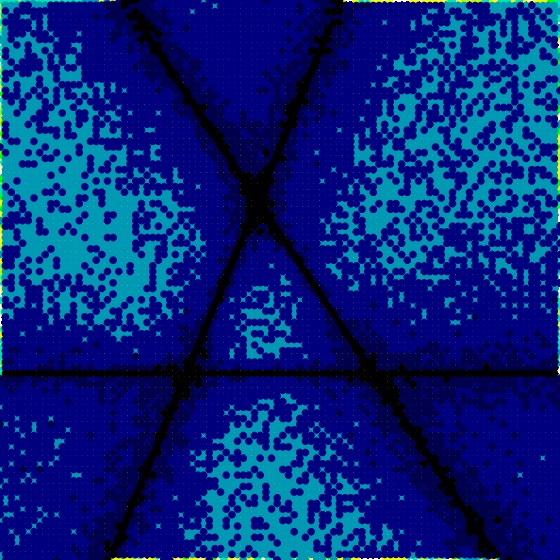
[data file 2to9pr48random2.dat] Although we do not obtain black, we do obtain dark blue, indicating that the fitting is working fairly well.
The first time we ran the tests for this example, we used the ALS algorithm at fixed rank rather than growing the rank (see ALS Performance Notes). That algorithm performed much worse, as illustrated in the Section A note on ALS failure.